Position Information Emerges in Causal Transformers Without Positional Encodings via Similarity of Nearby Embeddings (COLING 2025)
We propose a new theory of how position information can be stored in Transformers without positional encodings
Transformers work by encoding the input sequence into embeddings, and then repeatedly computing the next layer of the embeddings, using the embeddings from the previous layers. We review the use of positional encodings, and show how we think positional information can be stored in Transformers with causal attention.
The need (?) for positional encodings
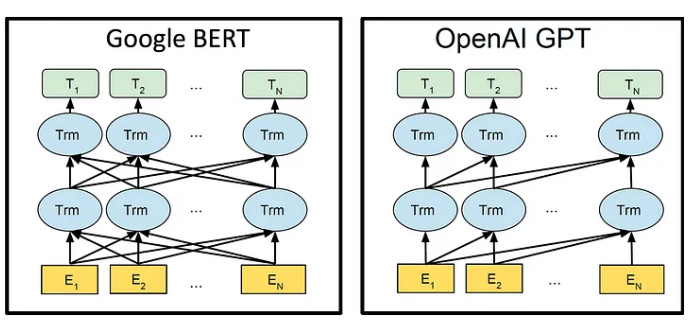
The top layer (the T units above) can be used to make a prediction. Usually, if we want to predict probabilities for the next token in the sequence
, we use Tn.
You can see that in the original BERT architecture, there is no way to distinguish the input sequence
from input sequence
For tasks where you don’t want the output to be invariant1 to permutation, that obviously wouldn’t work. The solution was to add, to each, positional encodings — vectors that encode the position of the token in the sequences.
You don’t need positional encodings
Irie et al. (Interspeech 2019) found that actually, for Transformers that use GPT-like causal attention, where token i in the next layer are only computed using tokens 1, 2, …, i in the previous layer, positional encodings are not necessary for tasks that require position information: position information in the transformer is stored anyway. (Haviv et al. (Findings of EMNLP 2022) popularized the finding).
Jason’s observation: nearby embeddings are similar, and this can explain how position information is stored
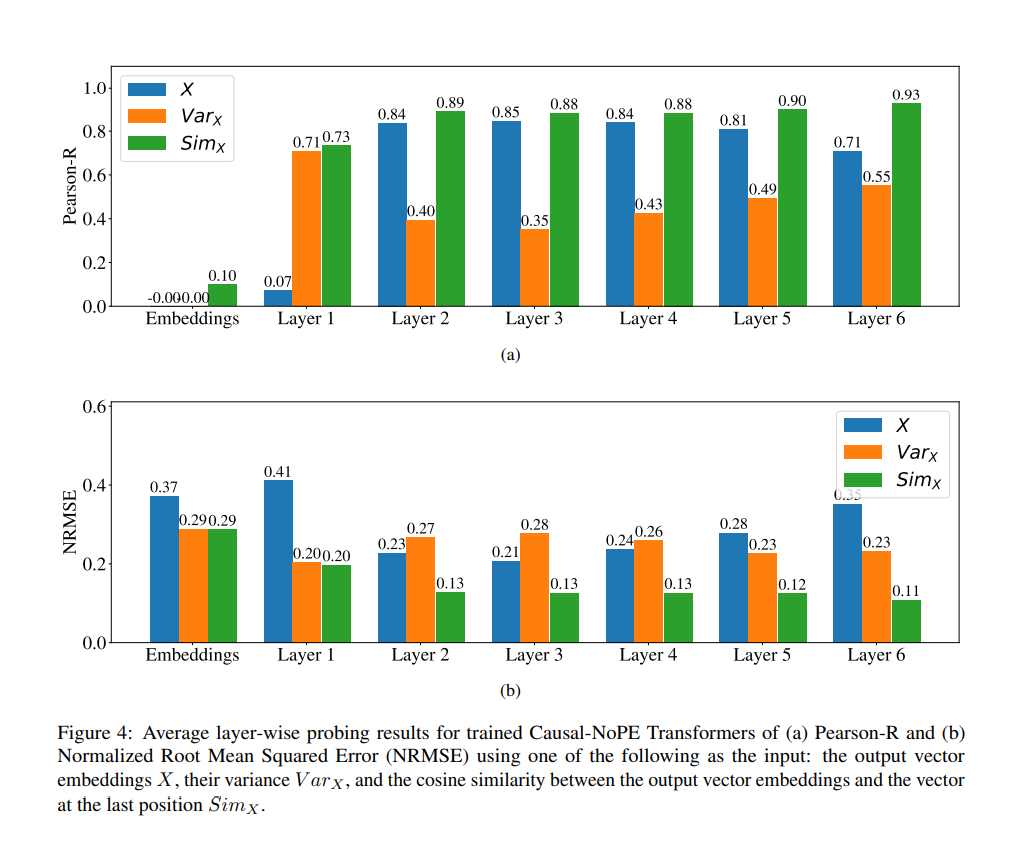
Sometime last winter, Jason made a striking observation: in both trained (on a variety of tasks) and untrained Transformers with causal attention, nearby embeddings were similar, in the cosine similarity sense.
As you see, nearby embeddings (except in the input layer) are more similar to each other than faraway embeddings.
You can intuitively see how this kind of structure might allow the Transformer to reconstruct the position in the sequence of any token, and we confirm this intuition by training neural networks on top the the correlation matrices above to reconstruct the position. We don’t do a perfect job, but we do a better job than if we were predicting the position just from the embedding or from an alternative theory of how position information can be stored (Chi et al. 2024).
How does this happen?
It’s not surprising that nearby embeddings are different: in the paper, we have a mathematical theory that accounts for the similarities in the first layer. In trained Transformers in the upper layers, you’d expect similarity based on the semantics of nearby embeddings: the semantics of a vector that summarizes tokens 1..k should be similar to the semantics of a vector that summarizes tokens 1..k+1.
Conclusion
We report progress on understanding how positional information might be stored in Transformers with no positional embeddings.
Technically, equivariant